Computer Programs in Seismology Tutorial

Introduction

The program hudson96 combines the effects of a layered crust at the source and receiver with ray theory in the mantle to create teleseismic synthetics for the signals near the direct P- or S-wave arrivals. One use of these is is better define the source depth of the earthquake. The tutorial HUDSON introduced the technique, discussed its use, and compared the Hudson synthetics to complete synthetics obtained using wavenumebr integration with a suitably flattened Earth model.

The purpose here is to focus on the applicability of the Hudson technique as a tool for estimating source depth. The concern is whether ignoring PcP and PP arrivals may affect the usefulness.

This will be addressed in several ways. First wavenumber integration synthetics for the AK135 model will be plotted on top of the P, pP, sP, PcP and PP travel times given by taup_time for the ZSS, ZDS, and ZDD Green's functions to indicate epicentral distance ranges for which the Hudson synthetics are adequate. Since the waveforms corresponding to a deviatoric moment tensor are a linear combination of these Green's functions, these comparisons will focus on the possible interference of the PcP and PP amplitudes on the P, pP and sP arrivals which are used to constrain the source depth.

This will be followed by a comparison of the Hudson and complete synnthetics at selected epicentral distances and depths. This comparison differs from that given in /eqc/eqc_cps/TUTORIAL/HUDSON/TESTAK135/index.html in that the effect of source duration will be factored in. At this stage of the documentation, quantitative measures of the differences will not be performed.

Questions and Tests for Implementation

• In the implementation of the NEIC bbDEPTH and SynDepth, a source time function is convolved with the Hudson synthetics for a given moment tensor. What is the time window used for a comparison between the observed and predicted traces, e.g., T_sP - T_P + source duration? This is important to avoid later arrivals not included in the Hudson synthetics. A side effect of a varying window is that the goodness of fit must be designed so as to not be sensitive to the different window lengths which will be a function of epicentral distance and source depth.
• Using a typical distrubution of epicentral distances and azimuths, create a synthetic waveform using the complete Green's functions in HYDRA. Given this "network" create events have different moment tensors, depths and source time functions. then compare the SynDepth depth and source time function to the known input. This will point out limitations and thus lead to rules for the use of SynDepth results.

Tests

• Travel time comparison
• Waveform record sections with focus on signal duration and interference
• Waveform record sections with focus on amplitude agreement between the WK and Hudson synthetics

Rules for use

• Suggested rule for use as function of arc distance, source depth and source duration

  Travel time comparisons

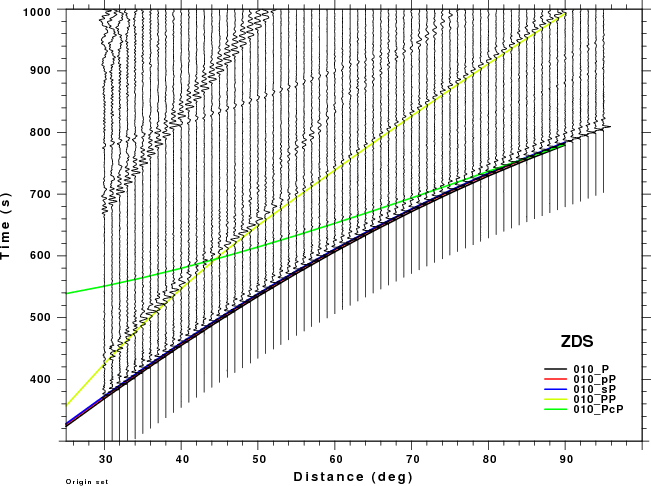
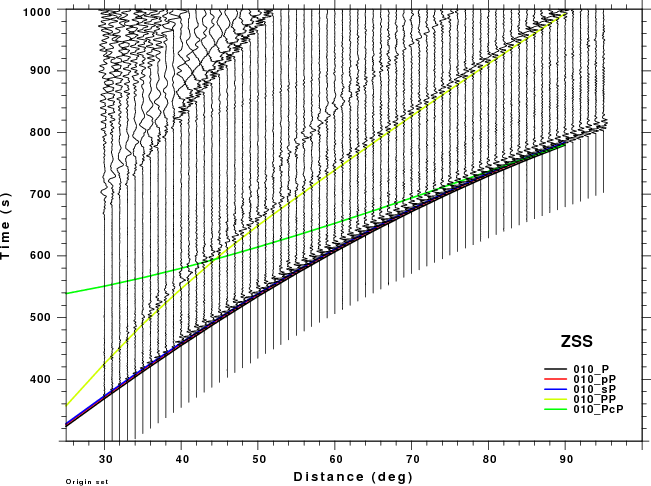
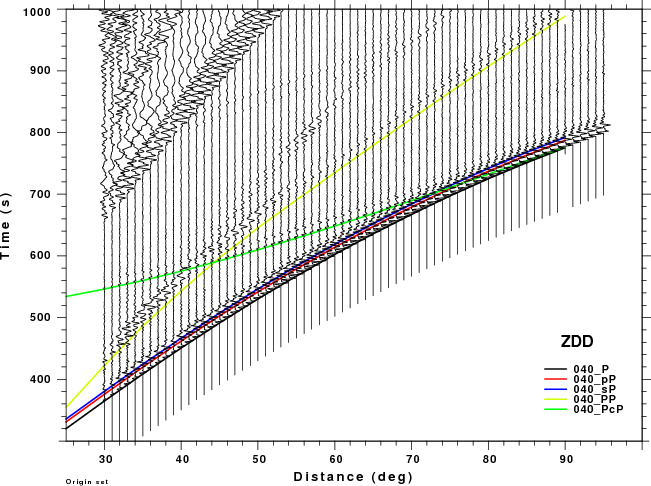
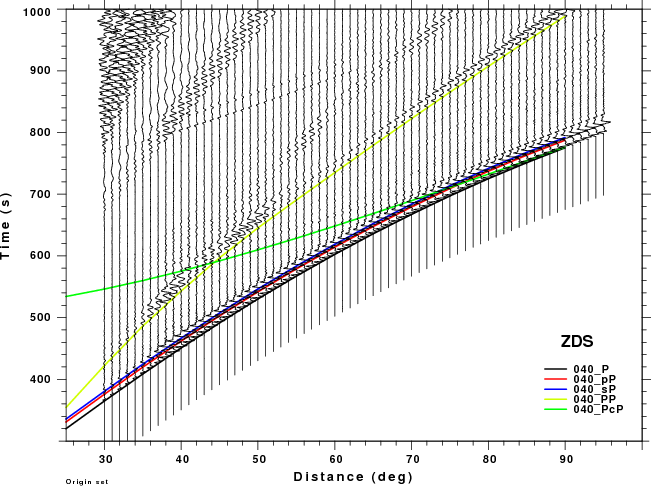
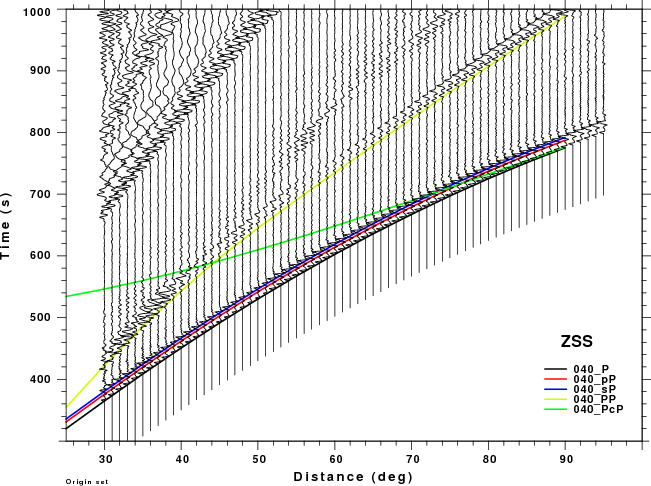
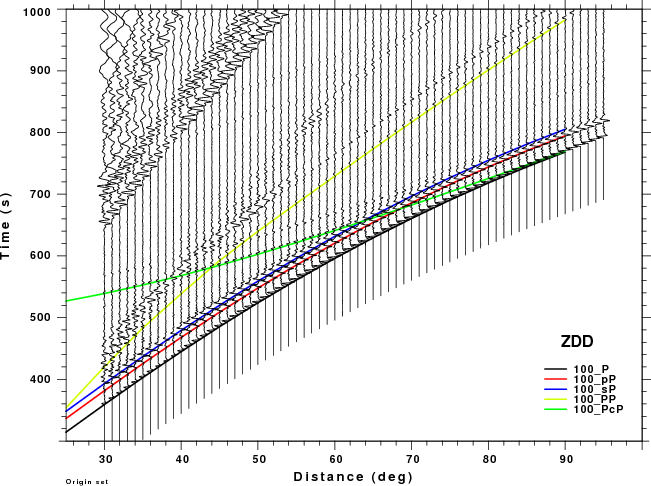
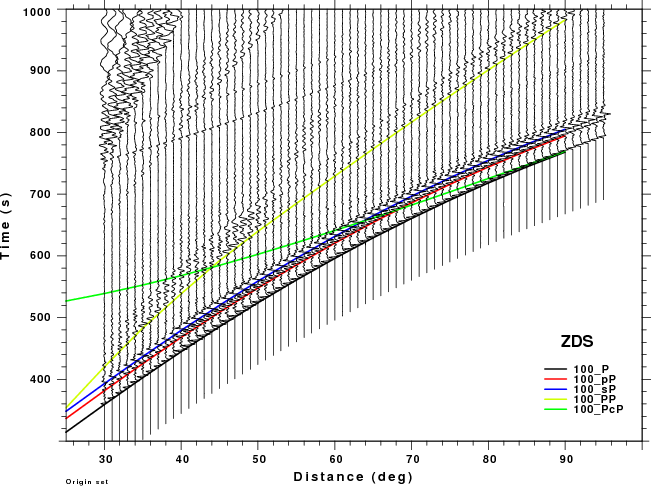
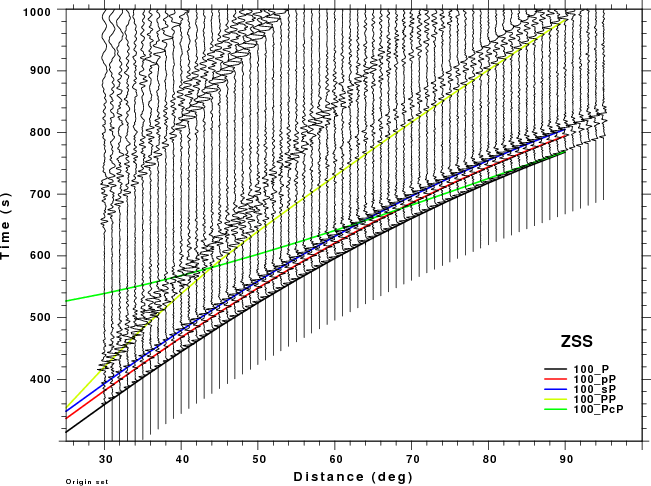
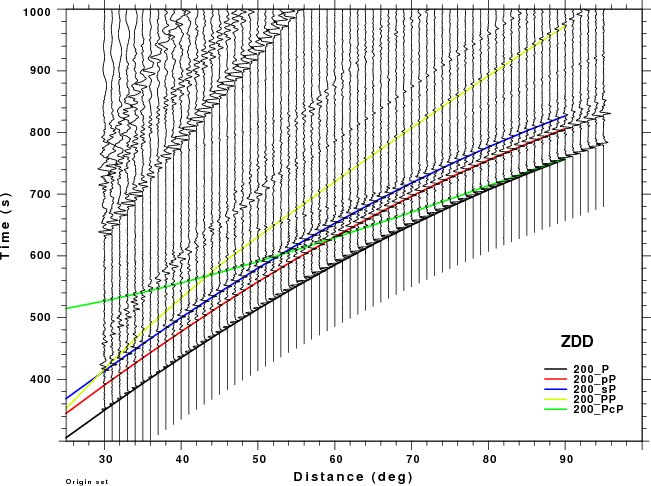
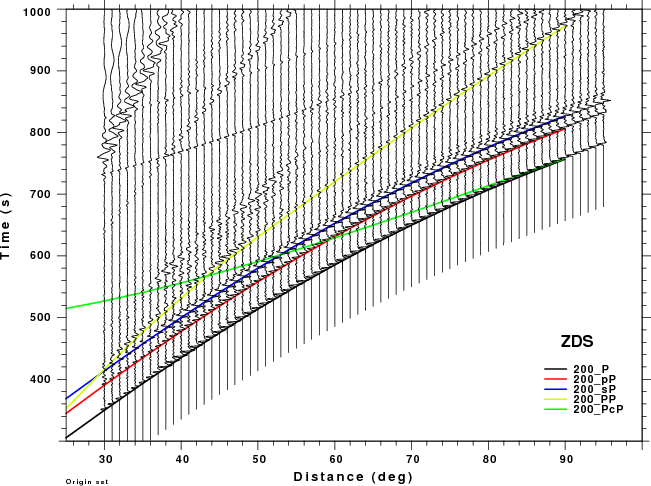
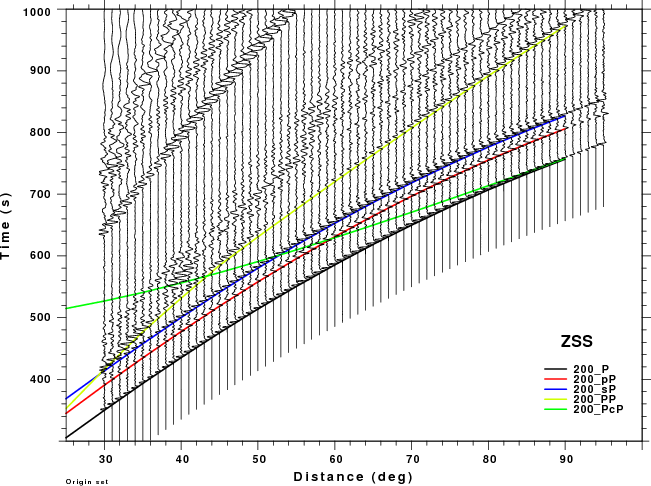
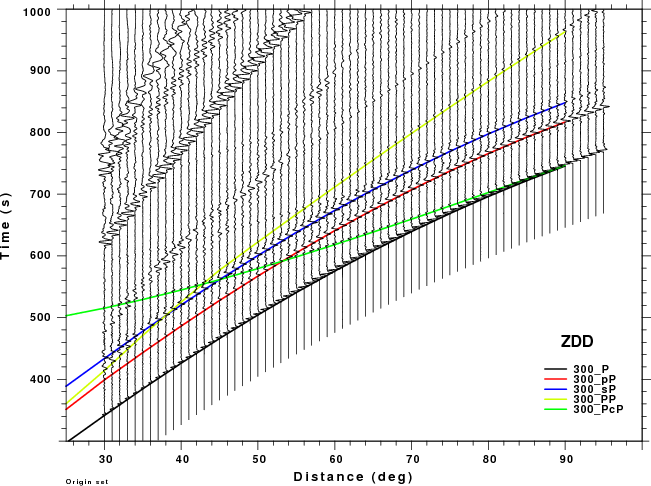
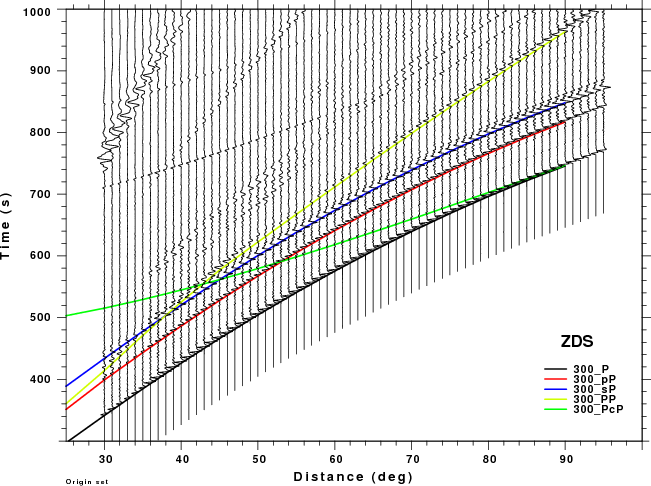
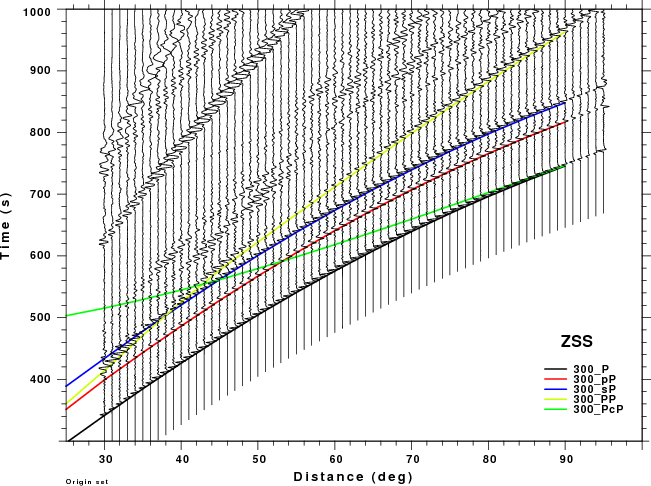
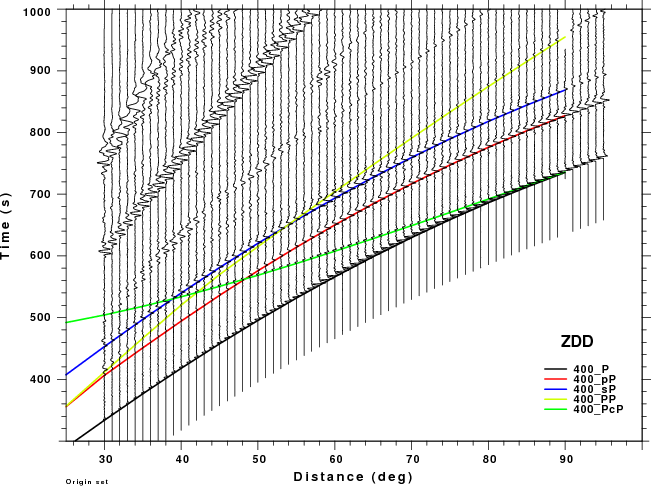
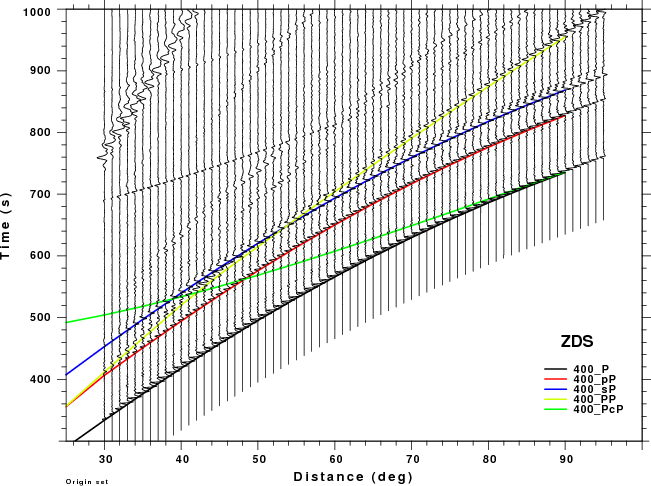
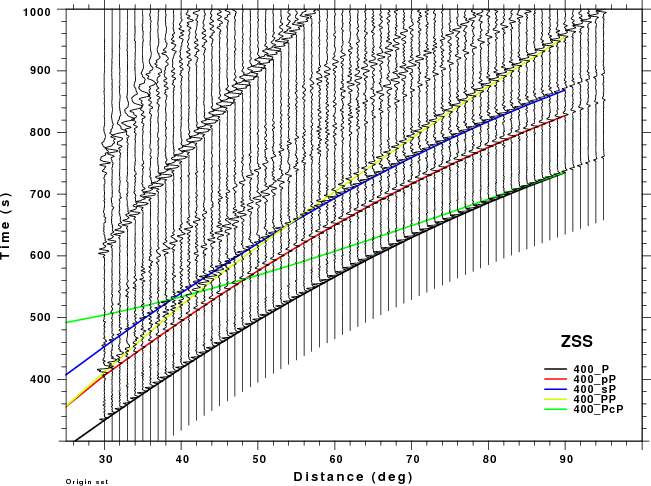
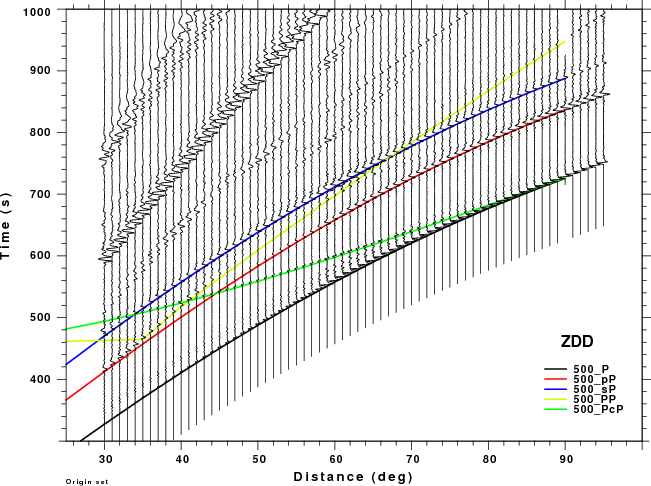
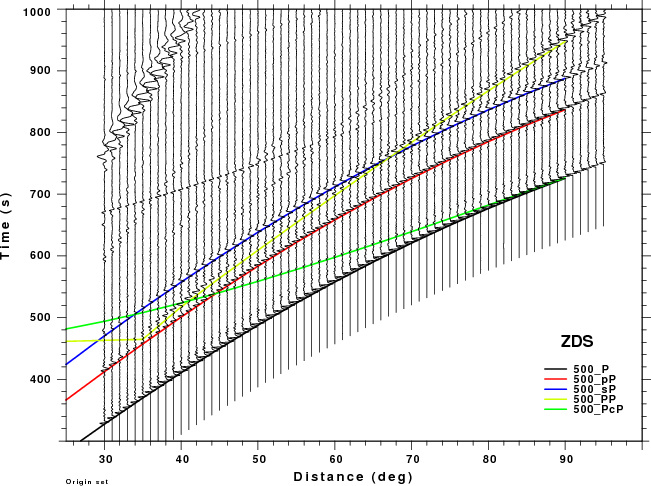
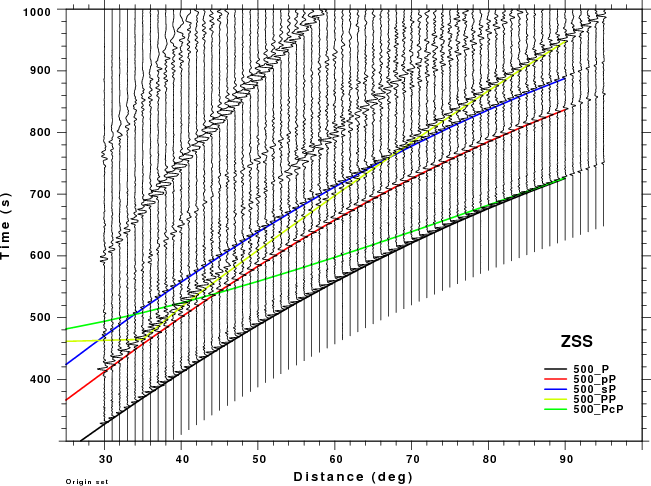
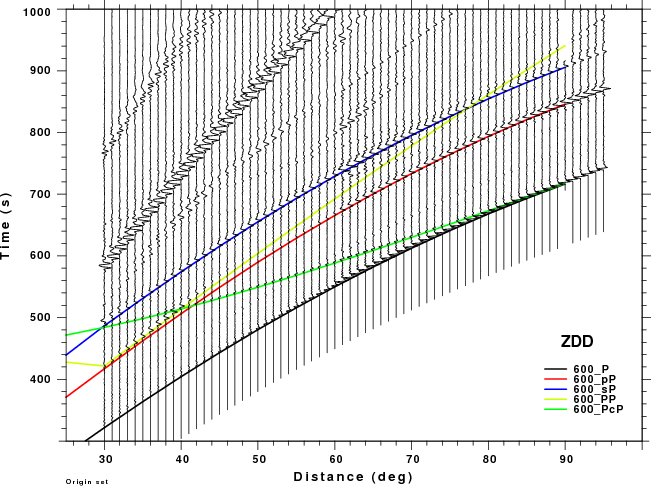
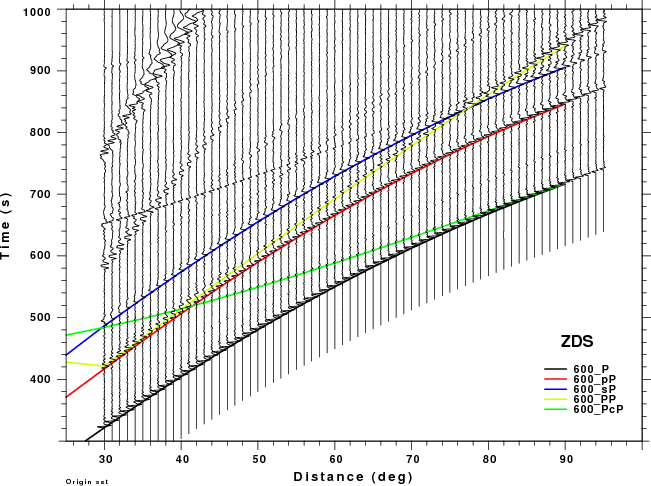
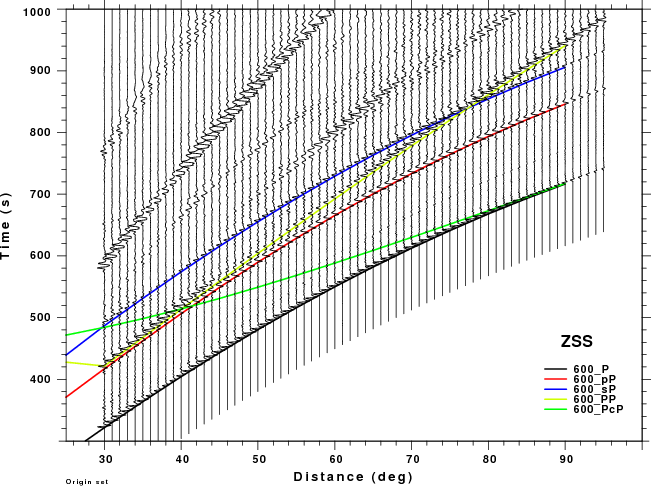
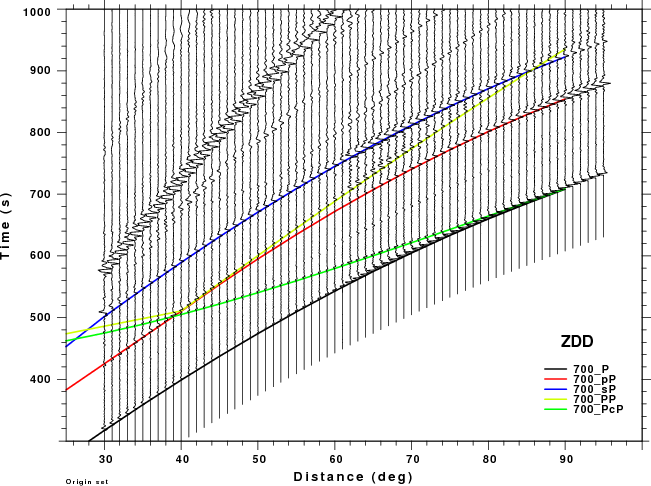
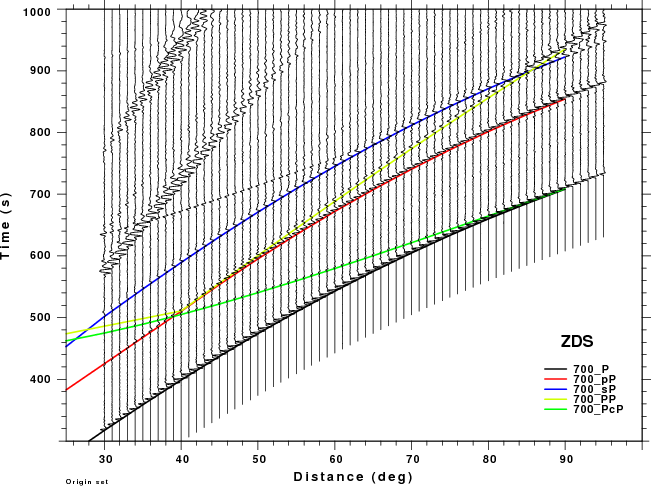
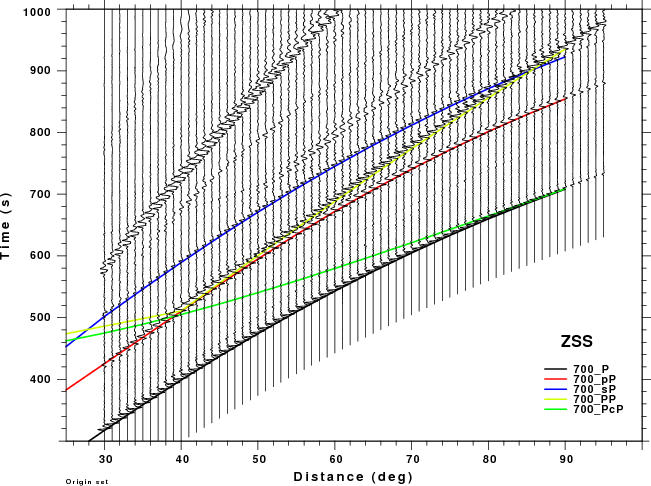
  The figures shown here are arranged horizontally by Green's function and vertically by depth. The depths are 1, 10, 40, 100, ...,700 km. In the figures, the legend that the bottom right of each figure giv ethe Green's function, a color code for the phase and an indication of the depth, e.g., 010_PcP is for a source depth of 10 km.

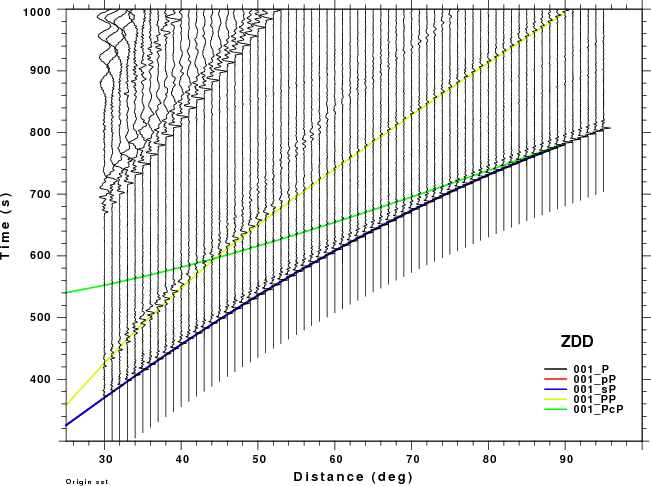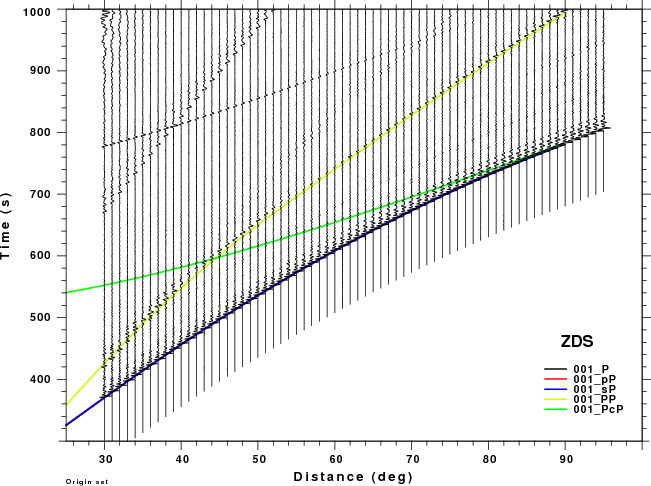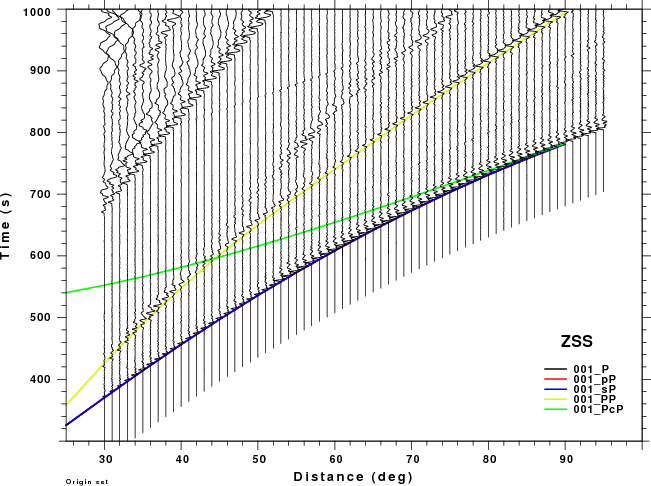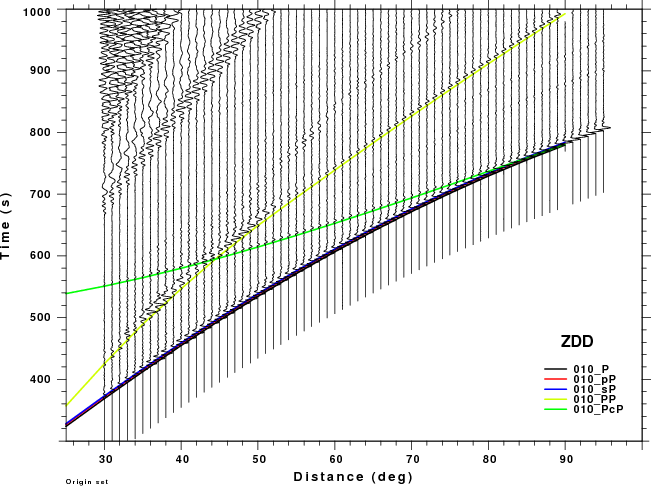  Discussion

  The following table attempts to summarize the information presented in these figures.

  Depth (km)	PcP	PP
  1	no concern, low amplitude	No problem if processing window is lest than 50sec at short distance.
  10	no concern, low amplitude
  40	no concern, low amplitude
  100	no concern, low amplitude	May be a problem for Δ < 35°
  200	no concern, low amplitude	Problem Δ<40°
  300	no concern, low amplitude	Problem Δ<50°
  400	no concern, low amplitude
  500	no concern, low amplitude	Interesting. For ZSS strong interference with pP for Δ <50° and sP after 70°
  600	no concern, low amplitude	PP interferes with pP as short distances and sP at larger distances. Significant fot ZSS.
  700	no concern, low amplitude	PP interferes with pP for Δ > 50° especially for ZSS

  Summary: At larger distances PP can interfere significantly with sP. At shorter distances PP may ba a problem if the tiem window used for processing to too large.

  Trace comparisons for different source durations

  These plots focus on the time window that the Hudson synthetics adequately represent the teleseismic signal. The Hudson synthetics are compares to the full wavenumber integration synthetics for the ZDD, ZDS and ZSS Green's functions. These figures provide the basis for defining the distance range for which the Hudson sysnthetics are adequate, e.g., when the effect if PP does not distort the signal, as a function of source depth, epicentral distance and source duration.

  There are four displays. The first is of the "high frequency" Green functions. This is misnomer, since the wavenumber integration synthetics have a sample interval of 1.0s, and their source function has a duration of 4s. The others have had the synthetics convolved with a triangular pulse of dureation 5, 10 or 15s, to represent the signal expected for increasingly larger earthquakes, respectively.

  • Record sections of Green's functions as a function of source depth.
  • Record sections of Green's functions convolved with a 5 second triangle as a function of source depth
  • Record sections of Green's functions convolved with a 10 second triangle as a function of source depth
  • Record sections of Green's functions convolved with a 15 second triangle as a function of source depth

  Discussion

  These record sections provide a more detailed comparison of the WK and Hudson synthetic than was possible in the travel time plots above, whose primary purpose was to identify the PcP and PP phase on the synthetics. The expanded view in this section permits one to focus better on the appropriate distance range and on the signal interferences. The big problem for large depths is that the Hudson synthetics cannot model the PP hase which is strong on the ZDS and ZSS (verticla dip-slip nd vertical strike-slip sources, respectively). This interference might cause a "fuzziness" in the depth estimate.

  True amplitude trace comparisons for different source durations

  These plots focus on the amplitudes of the two types of synthetics. The previous figures scaled each trace to the same maximum amplitude on the plot. To examine the amplitude, a true amplitude plot is not presented since amplitudes differ with distance due to geometrical spreading and radiaion pattern. Instead a correction for 1/distance(km) is made. This permits the amplitudes at a given epicentral distance to be compared.

  The concludion is that the initial amplitudes agree very well. Thus either set of synthetics could be used for quantitative source studies using the initial arrivals near P.

  • True amplitude record sections of Green's functions as a function of source depth.
  • True amplitude record sections of Green's functions convolved with a 5 second triangle as a function of source depth
  • True amplitude record sections of Green's functions convolved with a 10 second triangle as a function of source depth
  • True amplitude record sections of Green's functions convolved with a 15 second triangle as a function of source depth

  Rules

  The comparison of the Hudson synthetics to the complete synthetics shows that the interference of the P, pP and sP sequence of arrivals with PP is a major limitation of the method. The following table is an attempt to codify the use of the Hudson synthetics for determining source depth.

  The criteria is simple. if the PP arrival occurs before the sP + Soource_Duration time, then do not apply the technique. Implicit in the table is that data are not used at Δ < 30° to avoid the upper mantle triplication of P.

  The source duration is a function of Mw. An approximate relation between the duration of the simple triangle function to moment magnitude is
  

          Mw       Duration(s)
          5            1.5
          6            5.0
          7           15.0
          8           50.0
  

  
  The Mw=8 should never be used, since the simple triangular puulse cannot represent the expected signal of an large extended source. Thus there must be some upper magnitude bound on the use of this technique.

   Source Duration    0.00000000     s
  H/G  30. 35. 40. 45. 50. 55. 60. 65. 70. 75. 80. 85. 90.
    1.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
   10.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
   40.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  100.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  200.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  300.  -   -   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  400.  -   -   -   -   -   Y   Y   Y   Y   Y   Y   Y   Y
  500.  -   -   -   -   -   -   -   -   Y   Y   Y   Y   Y
  600.  -   -   -   -   -   -   -   -   -   -   Y   Y   Y
  700.  -   -   -   -   -   -   -   -   -   -   -   -   Y
   Source Duration    5.00000000     s
  H/G  30. 35. 40. 45. 50. 55. 60. 65. 70. 75. 80. 85. 90.
    1.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
   10.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
   40.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  100.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  200.  -   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  300.  -   -   -   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  400.  -   -   -   -   -   -   Y   Y   Y   Y   Y   Y   Y
  500.  -   -   -   -   -   -   -   -   Y   Y   Y   Y   Y
  600.  -   -   -   -   -   -   -   -   -   -   Y   Y   Y
  700.  -   -   -   -   -   -   -   -   -   -   -   -   Y
   Source Duration    10.0000000     s
  H/G  30. 35. 40. 45. 50. 55. 60. 65. 70. 75. 80. 85. 90.
    1.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
   10.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
   40.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  100.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  200.  -   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  300.  -   -   -   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  400.  -   -   -   -   -   -   Y   Y   Y   Y   Y   Y   Y
  500.  -   -   -   -   -   -   -   -   -   Y   Y   Y   Y
  600.  -   -   -   -   -   -   -   -   -   -   -   Y   Y
  700.  -   -   -   -   -   -   -   -   -   -   -   -   Y
   Source Duration    15.0000000     s
  H/G  30. 35. 40. 45. 50. 55. 60. 65. 70. 75. 80. 85. 90.
    1.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
   10.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
   40.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  100.  Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  200.  -   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  300.  -   -   -   Y   Y   Y   Y   Y   Y   Y   Y   Y   Y
  400.  -   -   -   -   -   -   -   Y   Y   Y   Y   Y   Y
  500.  -   -   -   -   -   -   -   -   -   Y   Y   Y   Y
  600.  -   -   -   -   -   -   -   -   -   -   -   Y   Y
  700.  -   -   -   -   -   -   -   -   -   -   -   -   -
  

  Last Changed 14 FEB 2023